2016南平一中录取分数

【www.guakaob.com--中考】

2016南平一中录取分数(一)
2016年福建南平中考录取分数线已公布

2016年南平市区高中录取最低控制分数线通告

　　南平市区普通高中招生录取工作本着依据考生志愿，坚持综合评价、择优录取的原则，现将市区各普通高中学校新生最低录取控制分数线通告如下：

　　一、南平一中统招录取分数线：523.2分

　　二、南平一中定向招生各校录取分数线

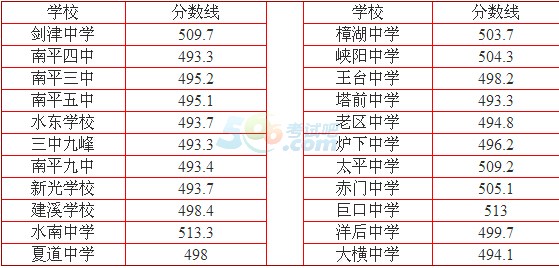
　　南平一中未完成定向招生计划，剩余指标的定向生录取分数线：499.7分

　　三、南平高级中学统招录取分数线：482.5 分

　　四、南平高级中学定向招生各校录取分数线

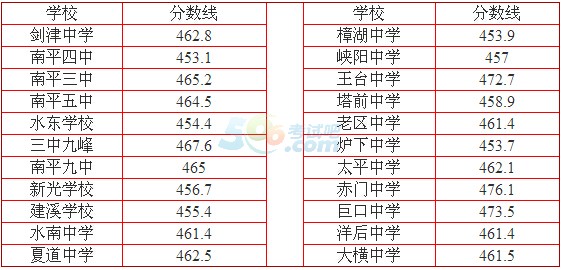
　　五、南平八中：390.8 分

　　六、南平九中：366.9分

2016南平一中录取分数(二)
2016年福建邵武中考录取分数线已公布

邵武市2016年普高录取分数线公告

　　根据《邵武市2016年招生工作意见》(邵招委[2016]1号)，在符合各高中录取条件的考生中，依考生投档分和志愿，择优录取。经研究决定，现将各校录取分数线公告如下：

　　一、邵武一中：

　　1、统招(不含定向生)：计划378人,实际录取379人，压线并列3人，超计划1人(占定向计划3人)，分数线508.1分。

　　2、定向招生：计划378人,实际录取377人，各校定向分数线如下表：

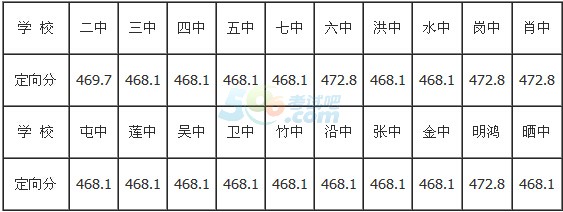
　　二、邵武四中： 计划486人，实际录取486人,分数线398.3分。

　　三、邵武七中： 计划400人，分数线320分。

　　注：

　　1、考生可登陆邵武市教育信息网http://www.swjyj.com 查询录取结果。

　　2、未被普高录取的考生，今年继续允许补报五年专志愿和中职学校志愿，补报志愿时间：7月22日8时--7月23日18时。考生可在规定的时间内，以原考生号和密码重新登录“南平市中招志愿填报系统”，进行补报五年专志愿和中职学校志愿，逾期不再受理。

2016南平一中录取分数(三)
南平2016年辅导机构高考成绩怎么样？

南平2016年辅导机构高考成绩怎么样

高考是学生人生中最重要的一场考试，关系到孩子未来的发展，家长们也在背后付出了非常多，包括时间和金钱。市面上有很多课外辅导机构，教学水平参差不齐。南平2016年辅导机构高考成绩怎么样？

100教育()是美国纳斯达克上市企业欢聚时代(NASDAQ:YY)旗下的在线教育品牌，董事长为雷军，投入10亿打造在线教育平台，聘请全国重点中学老师，为全国爱学习的学生提供一对一精心辅导。在今年高考中，不少学生取得理想的成绩，在此表示祝贺。希望更多学子能够在100教育接受最好的辅导，考上心目中理想中的高校。

附部分学生榜单：

在线教育真正能让孩子请到好老师

由于国内教育资源分布不均，优质教育资源都集中在经济发达地区、各个省市为数不多的重点中学，普通学校的学生得不到高素质老师的辅导教育；另一方面，由于学校老师工作繁忙，导致课外能够提供给学生的辅导时间较少。

100教育致力于打造一个高效的教育服务体系，来解决这些问题，服务更多的学生、家长。 对学生来说，通过网络自由选择全国各地的优秀老师，找到最适合他们的老师为他们辅导教学，让高效学习成为可能，让老师根据每个孩子的情况制定针对性的学习辅导计划，针对每个学生薄弱项，设计不同课程，不同的教学方案，足不出户，节省学习时间，提升学习效率。

对家长而言，不管身在何地，通过100教育的教学服务体系，家长可以远程旁听老师上课，随时监督教学效果，掌握孩子的学习状况，知道孩子有哪些薄弱环节。

轻松上课高效学习的教学理念

100教育突破地域限制，实现优质教育资源合理再分配，学生可以足不出户，轻松上课，高效学习。

(一) 重点中学老师授课

100教育从全国重点中学挑选有丰富教学经验的老师授课，老师筛选流程非常严格，首先要求老师必须拥有5年以上的授课经验，然后要进行专业知识考试、专业知识面试、授课技巧面试等一系列考查，最后还要在线试讲10次，好评率达90%以上的老师才会被聘用，通过率只有1.26%。

(二) 足不出户

学生足不出户即可接受100教育老师的一对一辅导，从而避免了雾霾、堵车等客观环境因素对学生造成的不良影响，为学生节省出更多学习时间。同时，100教育提供了课堂录像，方便学生随时回顾上课内容、查看随堂笔记，提升了学生的学习效率。

(三) 基于互联网的个性化教学

100教育借助互联网力量，真正做到个性化教学。利用大数据分析教学环链的每个环节、阶段考试中的错题集，准确暴露学习难点。教研团队通过分析课程录像，并结合授课老师的反馈，准确发现学生学习薄弱点，掌握学生学习进展，针对每个学生的薄弱项，量身设计不同课程。此外，100教育的老师都多次带过毕业班，能够快速判断学习情况，准确发现学生问题并制定相应的一对一辅导方案。

(四) 学习轨迹全记录

100教育通过云存储全面记录学生学习情况，利用云计算、大数据搜集整理学生学习的行为和结果数据，形成学生个人的学习轨迹数据，并借助智能诊断系统，帮助学生精确定位学习问题所在，从而进行有针对性的辅导教学。学生可以通过了解全程的学习轨迹随时调整学习计划和习惯，家长可以随时掌握学生的学习完成情况。

2016南平一中录取分数(四)
2015南平一中自主招生数学试卷答案

2015年福建省南平一中自主招生数学学科评分标准

一、选择题（本大题共10小题，每小题3分，共30分）

1.B；2.C；3.A；4.C；5.D；6.D；7. C；8. A；9.B；10.A.

二、填空题（本大题5小题，共20分）

11.；12.

；13.2；14.10

21【2016南平一中录取分数】



k1

a；15.0＜a＜

11

(填＂a＜＂不扣分) 66

三、解答题（本大题5小题，共50分）【2016南平一中录取分数】

16．（本题满分4分）

解：原式=32

(1)9(1)…………………2分 2

=3191 =4311 ……………………4分

17.（本题满分8分）

（1）证明：连OD，∵AD平分∠BA C，∴∠EAD=∠DAB，

又∵OA=OD，∴∠DAO=∠ADO，

∴∠EAD=∠ADO，∴OD//AE，………………2分 又DE⊥AE，∴OD⊥DE，

∵OD是⊙O的半径，∴DE是⊙O的切线………………4分 （2）解：连BD，∵AB为⊙O的直径，∴BD⊥AD,

在RtADB中，由勾股定理得，AD=8， ∵∠DBA+∠DAB=90， 同时∠DBA+∠DBF=90， ∴∠DAB=∠DBF， ………………6分 ∴ Rt△ADB∽Rt△BDF ,∴ 18.（本题满分8分）

解：当x > 0，原方程化为xaxa, x(a1)a 若a1时，方程无解，∴a1 ∴x

15ADBD

,∴ BF = ……8分

2ABFB

a

，由x > 0得a < 0或a > 1………………4分 a1

当x < 0，原方程化为xaxa, x(a1)a 若a1时，方程无解，∴a1

∴x

a

，由x < 0得-1 < a < 0 ……………………6分 a1

所以，满足原方程没有负根的取值范围是a1或a0．

综上：所求的a的取值范围是a1或a1 ……………………8分 19.（本题满分15分） 解：（1）如图1，连接AC交BD于O点，

∵菱形ABCD，∠ADC＝60°，∴△ACD与△ABC为等边三角形， ∵菱形ABCD的边长为2，∴DO=BO=

23, 2

当点E与点D重合时，点P为等边△ACD的外心

∴DP=

222DO,…………………2分 333

（第19题图1）

当点E与点C重合时，点P为等边△ABC的外心

114

BO333324DP……4分∴线段DP长的取值范围为33∴DP=DO

OPDO

（2）证明：如图

1，∵△ACD与△ABC∴AD=AC，∠ADE=∠ACE=60°， ∵四边形AFCE为⊙P的内接四边形，

∴∠AEC+∠AFC=180°,∵∠AED+∠AEC=180°, ∴∠AED=∠AFC,∴△ADE≌△ACF

∴AE=AF ……………………………………7分 ∵∠AFE=∠ACE=60°，

∴△AEF是等边三角形. ………………………9分 （3）

B

11为定值1．……………………10分 DMDN

当AE⊥CD时，△AEF面积最小， ……………11分

此时点E、F分别为DC、BC中点

连接AC交BD于点P，

（第19题图2） 解法一：如图2，设DM=x，DN=y，则CN=y-2，

∵BC∥AD，∴△GBP≌△MDP，∴BG=DM=x，∴CG=2-x， ∵BC∥AD，∴△NCG∽△NDM，∴

CNCG

，……………………………13分 DNDM

∴

y22x

，∴xy2x2yxy，∴xyxy，………14分 yx

∴

1111

1．…………15分 1，即

DMDNxy

解法二：

如图3，过点P作PI⊥DC于I，PJ⊥DA于J，

则PI=PJ=，

2

∵SDNPSDMPSDMN，………13分 ∴

111

DNPIDMPJDMDNsin60， 222

（第19题图3）

∴

1131， DNDMDMDN

22222211

1． …………15分 DMDN

∴DNDMDMDN， ………14分 ∴

20.（本题满分15分）

解：（1）如图1，设P（a，-2），

(i)当a=0时，点P与点A重合，这时OP的垂直平分线为y1， 0

此时∠AOP=∠MPO=0 得，M(0, -1),

(ii)当a ≠0时，设M（x,y） 由MP∥y轴，有xa，

(第20题图1)

∵M是线段OP的垂直平分线上一点∴MO 又MO

xy ，MPy2

22

222

∴xyy2，平方得，x4(y1)（y1）……………3分

综上,所求的函数关系式为x4y1.………5分

2

(2)由（1）知当点M在x4(y1)上时，作MG 垂直于y=-2于点G， 由（1）的推导过程得则︱MO︱=︱MG︱,

2

则︱MO︱+︱MT︱=︱MG︱+︱MT︱，………7分

作TF垂直于直线y=-2于点F，则︱MG︱+︱MT︱≥︱TF︱， 又T(1，2)，得︱TF︱=3，在 x4(y1) 中，令x=1得y即当点M的坐标为（错误！未找到引用源。1,值为4. ………10分

(3)不妨取m=1得直线为y=x ，取m=2得直线为y=2x -1，

联立两直线得点B(1,1) ……………………11分 （注：本题也可取其它的m值）

依题意，直线ymxm1(m0)和x4(y1)（y1）相交于C,D两 点，过点 B作BB垂直于x轴于点B,则B(1,0),过点 C作CC垂直于x轴于点C, 过点D作DD垂直于x轴于点D,设C((x1,y1),D((x2,y2),那么

/

/

/

/

/

/

/

2

3， 4

3

）时，︱MO︱+︱MT︱的最小4

2

C((x1,0),D((x2,0)， 不妨设x1<x2,

/

/

////

如图所示，∵CBDB,由相似比得CBDB，

∴1x1x21 ∴x1x22， ……………………13分 又联立直线ymxm1(m0)和x4(y1)

2

2

得到x4mx4m80， 由x1x22及韦达定理得4m2，∴

m

12

∴所求m的取值范围为m＜

O

F

(第20题图2)

1

且m0……………………15分 2

y

B O

B

D D

y

M

T

C

G

C

(第20题图3)

2016南平一中录取分数(五)
2016南平中考数学试卷

2016南平一中录取分数(六)
2015南平一中自主招生数学试卷

2015年福建省南平一中自主招生数学学科试卷

考试时间：90分钟 满分100分

一、选择题（本大题共10小题，每小题3分，共30分.每小题只有一个正确答案）

1.把多项式x22xyy21因式分解之后，正确的是（ ）.

A. (xy1)(xy1) B. (xy1)(xy1)

C. (xy1)(xy1) D. (xy1)(xy1)

2. 甲、乙两个工程队共同承包某一城市美化工程，已知甲队单独完成这项工程需要30天，若由甲队先做10天，剩下的工程由甲、乙两队合作8天完成．设乙队单独完成这项工程需要 x天．则可列方程是（ ）.2.

A. 1081011101 B.108x30 C.8()1 D.(1)x8 30x3030x30

3.右图的长方体是由A，B，C，D 四个选项中所示的四个

几何体拼接而成的，而且这四个几何体都是由4个同样大

小的小正方体组成的，那么长方体中第四部分所对应的几

何体应是（ ）.

A. B. C. D.

4.在数-1、1、2中任取两个数作为点的坐标，那么该点刚好在一次函数y=x-2图象上的概率是（ ）.

A. 1112 B. C. D. 2363

25.已知x1，x2是关于x的一元二次方程xxm0的两个不同的实数根，如果x1与x2同号，

那么m的取值范围是（ ）.

A. m0 B. 0m1 C. m11 D. 0m 44

6.如图，在平面直角坐标系xOy中，多边形ABCDEF的顶点坐标分别是A（-6，4），B（0，4）， C（0，2），D（2，2），E（2，-4），F（-6，-4）.若直线l经过点M（-3，0），且将多边形 ABCDEF分割成面积相等的两部分，则直线l的函数表达式是（ ）.

A.y

2015年南平一中自主招生考试 第 1 页（共 4 页） 13111113x B. yx C. yx D.yx 44434344

D B A

(第6题图) (第7题图)

7. 如图，在梯形ABCD中，A90，AB=7，AD=2，BC=3，如果线段AB上的点P使得以P、A、D为顶点的三角形与以P、B、C为顶点的三角形相似，那么这样的点P的个数是（ ）.

A. 1个 B. 2个 C. 3个 D.4个

8. 如图，在平面直角坐标系xOy中，设点M(x0，1)，点N是半径为1的⊙O上一动点，且始终有∠OMN＝45°，则x0的取值范围是（ ）.

A. 1x01 B. 

9.若函数y1122x0 C. 2x02 D.  x0222212和yaxbx(a0)的图象有且仅有两个不同的交点A(x1,y1)， x

B(x2,y2)，则下列判断正确的是（ ）.

A. a一定大于0 B. 当a < 0时，x1x20

C.当a >0时，x1x20 D.总有x1x20

10.如图，一个直径为1的小圆沿着直径为2

滚动，M和N是小圆的一条固定直径的两个端点.大圆内壁的一周，点M，N在大圆内所绘出的图形大致是（

A. B. C. D. 二、填空题（本大题5小题，共20分）

11. C B l1 l2 l3 3a111与3a是相反数，则a= ． aaa12.如图，已知l1∥l2∥l3，相邻两条平行直线间的距离相等，若等腰 (第12题图)

直角△ABC的三个顶点分别在这三条平行直线上，则sinα的值是 ．

2015年南平一中自主招生考试 第 2 页（共 4 页）

2016南平一中录取分数(七)
2016年南平市普通高中毕业班质量检查试卷 理科数学

2016年南平市普通高中毕业班质量检查

理科数学试题

（满分：150分 考试时间：120分钟）

注意事项：

1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。 2．答题前，考生务必将自己的姓名、准考证号填写在答题卡上。 3．全部答案答在答题卡上，答在本试卷上无效。 4．考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷

一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是

符合题目要求的.

2

0，Bx2x8，则AB (1) 集合Axx2x8≤





（A）(,2] （B）[2,3) （C）[4,3) （D）(,3]

(2) 已知i为虚数单位，若x2ixi62i，则实数x的值等于

（A）4 （B）－2 （C）2 （D）3 (3) 已知满足线性相关关系的两个变量x,y的取值如下表：

y0.95xa，则a 若回归直线方程为ˆ

（A）3.2 （B）2.6 （C）2.8 （D）2.0

x2y2

(4) 若双曲线221a0,b0的一条渐近线方程是3x2y0，则它的离心率

ab

等于

（B）2（C） （D）

2

（A） 3 3

(5) 一个算法的程序框图如图所示，若该程序输出的结果

为10，则判断框中应填入的条件是 （A）k≥－3 （B）k≥－2 （C）k＜－3 （D）k≤－3 (6) 数列an中a1

an11

,an1,记数列的前n项

an213an

（B）77

（D）126

和为Tn，则T8的值为 （A）57 （C）100

(7) 某几何体的三视图如图所示，则该几何体的

体积为 （A）

10

3

（B）

8

3

正视图

侧视图

（C）4 （D）3

0,xy≥



(8) 设为不等式组xy4≥ 0,(m0)表示的

xm,≤

平面区域.若的面积为9，则m= （A）8 （B）6 （C）4 （D）1

10

2

俯视图

10

(9) 已知正实数m，若， xxa0aammx)x)aammx)x)a10a(10m(mx)x)0a1(1(2(2(

其中a8180，则m值为

（A）4 （B）2 （C）3 （D）6

(10) 已知球O的一个内接三棱锥PABC，其中ABC是边长为2的正三角形，PC为

球O的直径，且PC4，则此三棱锥的体积为

（C

（B）

（D

(11) 过抛物线y22px(p0)的焦点F的直线l与抛物线在第一象限的交点为A，与

（A

抛物线的准线的交点为B，点A在抛物线的准线上的射影为C，若，【2016南平一中录取分数】

48，则抛物线的方程为 （A）y216x （B）y28x （C）y242x （D）y24x

19

(12) 已知x0,y0,且4xy26，则函数F(x,y)4xy的最大值与

xy

最小值的差为

（A）24

（B）25

（C）26

（D）27

第Ⅱ卷

本卷包括必考题和选考题两部分。第（13）～第（21）题为必考题，每个试题考生都必须作答。第（22）～第（24）题为选考题，考生根据要求做答。 二、填空题：本大题共4小题，每小题5分.

(13) 函数fxsinxcosx,x[0,]的值域是

(14) 在1和16之间插入n2(n≥3)个实数，使这n个实数构成递增的等比数列，若记这

n个实数的积为bn，则b3b4bn

2

3x2sinx3

(15) 曲线y的对称中心坐标为2

x1

(16) 在AOB中，OA1,OB2,AOB120，MN是过点O的一条线段，且

OMON3，若22(1),(R)，则的最小值

为 .

三、解答题：解答应写出文字说明、证明过程或演算步骤. (17)（本小题满分12分）

在△ABC中，角A,B,C的对边分别为a,b,c.若sinABsinC2sinA. （Ⅰ）求角B的值；

22

（Ⅱ）若b2，求ac的最大值，并求取得最大值时角A,C的值.

(18)（本小题满分12分）

如图，在直角梯形ABCD中，AB//CD，DAB9090，点E、F分别在CD、

AB上，且EFCD，BEBC，BC1，CE2.现将矩形ADEF沿EF折起，使平面ADEF与平面EFBC垂直. （Ⅰ）求证：CD∥面ABF；

（Ⅱ）当AF的长为何值时，二面角ABCF的大小为30.

(19)（本小题满分12分）

某研究性学习小组为了解学生每周用于体育锻炼时间的情况，在甲、乙两所学校随机抽取了各50名学生，做问卷调查，并作出如下频率分布直方图：

DE

E

A

B

D B

甲图

乙图

（Ⅰ）根据直方图计算：两所学校被抽取到的学生每周用于体育锻炼时间的平均数； （Ⅱ）在这100名学生中，要从每周用于体育锻炼时间不低于10小时的学生中选出3

人，该3人中来自乙学校的学生数记为X，求X的分布列和数学期望.

(20)（本小题满分12分）

3x2y2

已知点P(1,)在椭圆C:221(ab0)上,过椭圆C的右焦点F且垂

2ab

直于椭圆长轴的弦长为3.

（Ⅰ）求椭圆C的方程；

（Ⅱ）若MN是过椭圆C的右焦点F的动弦（非长轴），点T为椭圆C的左顶点，

记直线TM,TN的斜率分别为k1,k2.问k1k2是否为定值？若为定值，请求出定值；若不为定值，请说明理由.

(21)（本小题满分12分）

设函数f(x)ln(1x).

（Ⅰ）若曲线yf(x)在点(0,f(0))处的切线方程为yg(x)，当x≥0时，

x(1tx)

，求t的最小值；

1g(x)

1111*

ln2. （Ⅱ）当nN时，证明：

n1n22n4n

f(x)≤

请考生在第（22）、（23）、（24）三题中任选一题作答。注意：只能做所选定的题目。

如果多做，则按所做第一个题目计分，做答时请用2B铅笔在答题卡上将所选题号后的方框涂黑。

(22)（本小题满分10分）选修4-1：几何证明选讲

如图，已知D点在⊙O直径BC的延长线上，

DA切⊙O于A点，DE是ADB的平分线，

交AC于F点，交AB于E点.

（Ⅰ）求AEF的度数； （Ⅱ）若ABAD，求

AD

的值. BD

(23)（本小题满分10分）选修4-4：坐标系与参数方程

在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系．已知曲线

，过定点P(2,4)的直线l

的参数方程为C:sin22cos

x2，若直线l和曲线C相交于M、N两点． (t为参数）

y4（Ⅰ）求曲线C的直角坐标方程和直线l的普通方程；

（Ⅱ）证明：PMMNPN成等比数列．

(24)（本小题满分10分）选修4-5：不等式选讲

已知函数f(x)xxa，其中a为实常数． （Ⅰ）若函数f(x)的最小值为2，求a的值；

（Ⅱ）当x0,1时，不等式x2≥f(x)恒成立，求a的取值范围．

本文来源：http://www.guakaob.com/xuelileikaoshi/655502.html